The new version of SimOne 2.5 is now available
What’s new in SimOne 2.5
Laplace sources
- Functional voltage and current sources, defined with Laplace transfer function are now moved to a separate component group in the Schematic. Each Laplace source has its own graphical symbol.
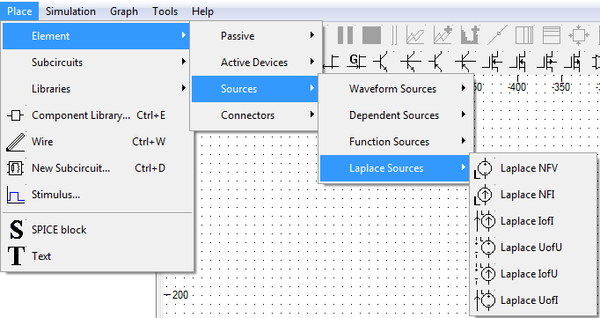
- New algorithms for convolution integral computation in Laplace sources have been added. Previously used algorithms get more manually chosen parameters.
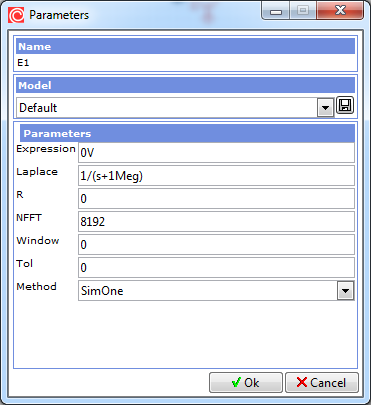
| Parameter | Description | Default value | Unit |
| Laplace | Laplace transfer function | 1/(s + 1Meg) | |
| R | Inner resistance | 0 | Ohm |
| NFFT | Number of points used for Inverse Fourier Transform | 8192 | — |
| Window | The interval of non-zero values of the transfer function in time-domain | Tend | sec |
| Tol | Minimal absolulte value of the function in the convolution integral | 0 | — |
| Method |
Numerical method for computation of Inverse Laplace Transform and the convolution integral. Three methods are available: - SimOne — the original method - IFT — Inverse Fourier Transform usage for ILT and trapezoidal rule for the convolution integral - Euler — Fourier-series method with Euler summation for ILT and and trapezoidal rule for the convolution integral |
SimOne |
- The transfer function can be given as a table of values. The special functions with “freq_” prefix are used for this.
Periodic Steady-State
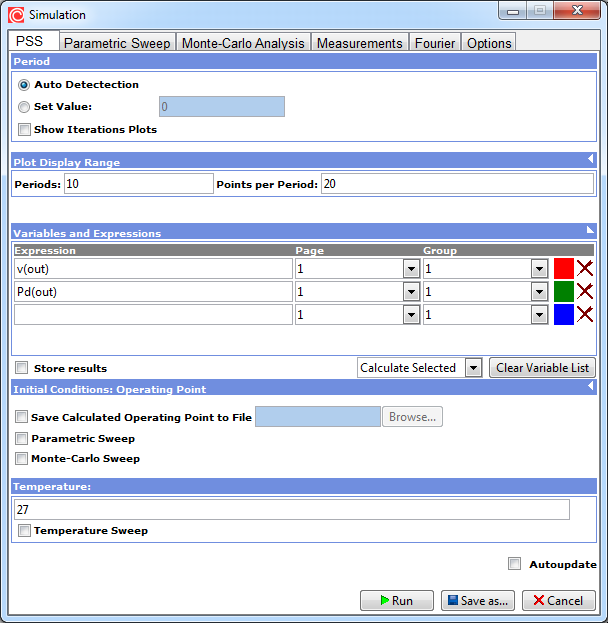
Periodic Steady-State analysis has a new interface.
- Time interval for plotting the graphs is now set in number of periods. The default value is 10.
- The maximal time step is set with minimal number of steps per period, the default value of which is 20.
Piecewise Linear input signals
New parameters for Piecewise Linear (PWL) signals are available:
| Parameter | Description | Default value |
| PWL_Method |
PWL processing method - Standard SPICE method - SIMONE: tries to consider the PWL signal as points of some smooth signal |
SIMONE |
| PWL_BPRELTOL | Relative tolerance for SIMONE method comparison of PWL slopes | 1 |
| PWL_BPABSTOL | Absolute tolerance for SIMONE method comparison of PWL slopes | 1e-6 |
Graphs
- Graphs axes can be switched between Linear/Logarithmic scales
| X axis in logarithmic scale |
Main menu: Graph → Log X
Icon: |
| Y axis in logarithmic scale |
Main menu: Graph → Log X
Icon: |
- It is possible to choose the view area of graphs manulally:
| Set the view borders for a group of traces |
Main menu: Graph → View rectangle… Icon: |
- Grpahs can be imported from SimOne simulation data files.
Mathematical expressions
New functions for integral transforms are added:
| laplace | laplace(f(x), H(s)) — the convolution of f(x) with the transfer function H(s) given in s-domain. Uses SimOne method. |
| laplace_smn | laplace_smn(f(x), H(s)) — same as laplace. |
| laplace_euler | laplace_euler(f(x), H(s), mtol) — the convolution of f(x) with the transfer function H(s) given in s-domain. Uses Fourier-series method with Euler summation. Values f(x) < mtol are ignored. |
| laplace_ift | laplace_ift(f(x), H(s), window, nfft, mtol) — the convolution of f(x) with the transfer function H(s) given in s-domain. Uses Inverse Fourier Transform. If window is specified, the frequency step is 0.5/window. The number of values used for IFT is equal to nfft. Values f(x) < mtol are ignored. |
| freq_db | freq_db(f(x), w1, db1, deg1, …, wn, dbn, degn) — the convolution of f(x) with the transfer function given in frequency-domain with discrete points as [frequency w, magnitude in decibels; argument in degrees] triples. |
| freq_db_deg | freq_db_deg(f(x), w1, db1, deg1, …, wn, dbn, degn) — same as freq_db. |
| freq_db_rad | freq_db_deg(f(x), w1, db1, rad1, …, wn, dbn, radn) — the convolution of f(x) with the transfer function given in frequency-domain with discrete points as [frequency w, magnitude in decibels; argument in radians] triples |
| freq_ma | freq_ma(f(x), w1, amp1, deg1, …, wn, ampn, degn) — the convolution of f(x) with the transfer function given in frequency-domain with discrete points as [frequency w, magnitude in absolute values; argument in degrees] triples. |
| freq_ma_deg | freq_ma_deg(f(x), w1, amp1, deg1, …, wn, ampn, degn) — same as freq_ma. |
| freq_ma_rad | freq_ma_rad(f(x), w1, amp1, rad1, …, wn, ampn, radn) — the convolution of f(x) with the transfer function given in frequency-domain with discrete points as [frequency w, magnitude in absolute values; argument in radians] triples. |
| freq_ri | freq_ma_rad(f(x), w1, re1, im1, …, wn, ren, imn) — the convolution of f(x) with the transfer function given in frequency-domain with discrete points as [frequency w, real part, imaginary part] triples. |
Bug fixes
- Laplace function in AC analysis is fixed
- Etc.



